Firstly, I would like to caution students regarding the use of solutions when preparing for exams. They are certainly a double-edged sword and since you are planning to invest an enormous amount of time, effort and money into getting a degree, it would be a good idea to use solutions properly from now on. In all cases you should only consult a solution once you think your answer is correct or if you have spent a significant amount of time trying to reach an answer. Coming up with your own conclusion after several minutes of independent thought is far more worthwhile than learning directly from the solution itself. You should also make sure you are critical of all solutions presented to you. Not only will this help your understanding, but solutions may have errors. Therefore if you find that you can't reconcile a solution with yours then take the time to get in touch with the author to discuss the discrepancy. For example, please do contact me if you have spotted a mistake below or would like further guidance on any of the questions.
For the 2020 solutions I have included the time taken next to each question. Note that there is wide variability in the time taken to solve each question. It is definitely a good strategy to be well rested for the exam with no cramming the night before! I will firstly set out a series of hints. Try to do the questions from these alone and if you are still having difficulty then scroll down to the full solutions.

Hints

Section 1

Part A

1. Write down the energy supplied and calculate the energy retained using $mc\Delta T$ then work out the difference. Time taken 0:37.

2. Form two simultaneous equations and solve Time taken 0:44.

3. Record how many alpha decays must have occurred then work out how much the proton number needs to increase by to reach lead. Time taken 0:30.

4. $5$ can be achieved by adding $3$ and $2$ in either order. Time taken 0:32.

5. Use $P=IV$ to work out the power supplied and received, dividing the latter by the former to calculate a percentage. Time taken 1:07.

6. Record the gradients of the lines by inspection. Time taken 0:22.

7. Apply $F=BIl$ and Fleming's left hand rule, taking care with the length over which the current flows. Time taken 1:22.

8. Save time by defining $y=\frac{x}{4}+3$ and solve the resulting quadratic. Time taken 1:28.

9. Apply conservation of momentum to work out the new speed and then the kinetic energies. Time taken 0:38.

10. Note that the constant term cancels. Expand in one step then complete the square. Time taken 0:51.

11. Use the graph to determine the final speed then apply force as the rate of change of momentum. Time taken 3:23.

12. Start with $N=\frac{k}{t^3}$. Leave $k$ as a product to aid cancellation. Time taken 0:52.

13. Try to find the wavelength from the information given without too much delay. The wave travels $vt$ but the distance between $P$ and $Q$ needs to be taken into account. Then apply $v=f\lambda$. Time taken 1:58.

14. Define the correct original price to be (say) $X$. Use percentage multipliers to work out the incorrect original price in terms of the correct original price, subtract $X$ and equate the result to $15$. Time taken 5:55 (several numerical/conceptual slips).

15. Use energy at the start - energy at the end = energy wasted. Time taken 1:29.

16. Visualise $SQ$ by inspection and apply trigonometry to the rightmost triangle. Time taken 0:47.

17. The energy at the start is elastic potential which is converted to gravitational potential and kinetic energy. Time taken 1:38.

18. Draw a rough diagram and visualise the two possible squares (whose orientations will be at $45^{\circ}$ to one another). Time taken 1:15.

19. Starting from Newton's second law, rewrite the mass as some initial mass minus a constant times time and rearrange for the acceleration 1:16.

20. Write the right-hand term of the quadratic formula and equate to $3$. Time taken 1:09.

Part B

21. The energy at the start is kinetic and gravitational potential, changing to kinetic energy and work done against friction. Time taken 0:49.

22. Substitute $1$ and $2$ in and solve the resulting equations. Time taken 0:40.

23. The pressure is the same at both pistons and is equal to force/area. Note that the area has gone up by a factor of 9. Apply work done = force $\times$ distance to work out how the distance moved by piston $Y$ should relate to that travelled by piston $X$. Time taken 0:59.

24. I sketched this but there was no need in retrospect as one of the functions is clearly beneath the other for the whole integral. Time taken 1:26 (inefficient method and numerical slips).

25. Determine the frequency from the graph, apply $c=f\lambda$ and note that the speed in water is greater than that in air which means the wave will be more 'stretched out' . Time taken 1:22.

26. Imagine what will happen to a line with gradient greater than $1$ - its gradient after the reflection will be between $0$ and $1$. Time taken 0:08.

27. Try not to be overfaced by the text and apply $F=BIl$ and moment $=$ force $\times$ perpendicular distance from pivot. Time taken 1:37.

28. Make two equations involving the sum of the arithmetic series, one for $20$ terms and the other for the first $40$ terms and solve. Time taken 1:24.

29. Conserve energy - the work done goes into increased kinetic energy and work done against the gravity (in this case it's best to think of work done against the component of weight acting down the slope). Time taken 1:38.

30. Draw a sketch and, taking the base of the triangle to be vertical, write this base in terms of $m$ and calculate the height as $2$ and solve. Time taken 2:22.

31. Use $P=IV$ to work out the current then $P=I^2R$ for the power. Time taken 1:27.

32. Note that the information given about the sequences implies that their common ratios are negatives of one another. Work out these common ratios and the first term then apply $S_{\infty}=\frac{a}{1-r}$. Time taken 3:27.

33. Work out the time taken to stop the ball, then use the average velocity to work out how far the ball travelled while it was being slowed down then double the result. I recommend keeping $a$ until the last step and focus on the leading digits of the answer rather than its precise value. Time taken 2:48.

34. After differentiation, the resulting quadratic requires a discriminant which is greater than zero. Time taken 1:23.

35. Form two equations using Hooke's law applied to each spring. Subtract these to take advantage of the $4cm$ given and calculate the spring constant then apply $\frac{1}{2}kx^2$. Time taken 1:47.

36. Make a mental note that $cosx=0$ solves this equation. Use $cos^2x+sin^2x=1$ to write the equation in terms of just one of $sinx$ and $cosx$ then draw a sketch. Time taken not recorded (probably less than a minute).

37. Equate the change in momentum to the area under the graph to find the velocity and apply $KE=\frac{1}{2}mv^2$. Time taken not recorded (probably about 1.5 minutes).

38. If it helps to cut down the amount you write, define $log_{10}x$ as $y$ and don't fall into the trap of thinking that the logarithm of a number can't be negative. Time taken 1:30.

39. Apply Kirchhoff's laws (mentally, not written down) to realise that the voltage around the lower middle loop must be $0$ then use potential dividers. Time taken not recorded (probably about 2 minutes).

40. Read the question carefully and differentiate twice. Note that the third derivative is negative so the only stationary point must be a maximum. Time taken 1:10.



Section 2

1. Work out the spring constant of the combination and then the load. Note that both springs each support this load because they are in series. Time taken 2:07.

2. Apply $R=\frac{\rho L}{A}$ and divide by $12$. Time taken 0:46.

3. Note that the time taken is enlarged by a factor of the refractive index. Apply this and use $ Time=\frac{Distance}{Speed}$. Time taken 1:05.

4. Work out the mass of the cube, followed by the extension of the spring in terms of $k$ then apply $EPE=\frac{1}{2}kx^2$. Time taken 3:57.

5. Evaluate how long the flight must be from the information given then apply SUVAT horizontally and vertically. Time taken 6:17.

6. Apply the same definition of amplitude for a transverse wave (the maximum displacement from the equilibrium position) to this longitudinal wave. Time taken 2:40.

7. Using the energy given, work out the initial velocity of the spaceship. Then calculate the new velocity after the impulse, find the change in Kinetic Energy and divide by the time taken. Time can be saved by using difference of two squares. Time taken 2:08.

8. Apply $Pressure=\frac{Force}{Area}$. Time taken 0:44.

9. Form two equations from the information given and solve. Time taken 1:21.

10. Apply $Power=Force \times Velocity$ to work out the resistive force then add this to the component of weight down the slope. Time taken 1:14.

11. Work out the possible resistances in terms of a unknown resistance, say $R$, and use trial and improvement to ascertain which of the possibilities correspond to those given in the question. Time taken 6:22 (Question misread in that I tried to do this with four resistors instead of 3).

12. Use Ohm's law to work out the resistance of the LDR at the initial intensity of light. Note that the resistance of the LDR must increase as a result of the dimming of the light and work out the potential differences across the two components then apply potential divider theory. Time taken 2:06.

13. Noting that the cord now takes the shape of an isosceles triangle, it can be observed by inspection that its length had increased by a factor of $\sqrt2$. The extension and then the Elastic Potential Energy follow from this. Time taken 3:02.

14. Recall that force is the rate of change of momentum. Time taken 0:48.

15. Differentiate to find the velocity as a function of time, from which you can work out the initial and final velocity. Applying difference of two squares may save some time in the final calculation. Time taken 1:05.

16. The relation between the refractive indices in media $P$ and $R$ are the same whether the light travels through $Q$ or not. Use the ratios given to find the ratio of speeds in medium $P$ to $R$ and note that the ratio of refractive indices will be this ratio reversed since speed is inversely proportional to refractive index. Once this has been obtained, Snell's law can be applied directly to media $P$ and $Q$. Time taken 2:40.

17. The horizontal paths are straightforward to deal with but for the vertical paths, form right-angled triangles to work out the resultant speed. Time taken 1:24.

18. Use the Young's Modulus formula to work out the extension then apply Energy stored $=\frac{1}{2}Fe$. Time taken 2:10.

19. Note that the net displacement is zero therefore the journey is 'there and back again' with a greater speed on the return journey. Time taken 0:58.

20. Find the potential difference across the variable resistor and multiply by $I$ to yield an expression for the power dissipated. Differentiate this and set it equal to zero to find a relationship between $E$, $k$ and $I$. Substitute this into an expression for $R$ found by applying Ohm's law to the potential difference across the variable resistor. Use the relationship between $E$, $k$ and $I$ again to find an answer in terms of $k$ and $E$. Time taken 10:13.



Full solutions

Section 1

Part A

1. Write down the energy supplied and calculate the energy retained using $mc\Delta T$ then work out the difference. Time taken 0:37.
By inspection, the energy supplied is $1500J$. The energy retained by the tip is $mc\Delta T=2\times 400\times 0.2$ where I have multiplied the mass by $1000$ and divided the temperature by $1000$ to save time by writing less. This equates to $160J$ retained so the answer is $1340J$
2. Form two simultaneous equations and solve Time taken 0:44.
$2a+3c=20$
$2a+2c=17$ where I have divided the second equation by $2$ before writing it.
$c=3$
$a=5.5$
$33+6$
3. Record how many alpha decays must have occurred then work out how much the proton number needs to increase by to reach lead. Time taken 0:30.
The mass number has decreased by $32$ so there must have been $8$ alpha decays (recall that beta decays don't change the mass number). $8$ alpha decays leave us with a proton number which is $6$ below what it should be therefore there are $6$ beta decays.
4. $5$ can be achieved by adding $3$ and $2$ in either order. Time taken 0:32.
There are $4$ sectors with $3$ in, so the probability of spinning a $3$ is $\frac{1}{2}$. There is only one sector with a $2$ in so the probability of this is $\frac{1}{8}$.
$\frac{1}{2}\times \frac{1}{8}\times2=\frac{1}{8}$
5. Use $P=IV$ to work out the power supplied and received, dividing the latter by the former to calculate a percentage. Time taken 1:07.
The two powers are $8\times10^8$ and $6.4\times10^8$. At this point look at the answers rather than do any calculations since this is clearly $80\%$ not $20\%$. The energy wasted per minute is $8\times10^8\times0.2\times60$ which starts $96...$
6. Record the gradients of the lines by inspection. Time taken 0:22.
The gradients are:
$-\frac{1}{3}$
$\frac{1}{3}$
$3$
-$\frac{2}{3}$
7. Apply $F=BIl$ and Fleming's left hand rule, taking care with the length over which the current flows. Time taken 1:22.
Index finger into the page, Second finger down the page shows the force as being to the right. For the force, the length of the wire in the field is $12cm$, not $20cm$.
$a=\frac{F}{m}=\frac{0.5\times2.4\times0.12}{0.04}=\frac{1.44}{0.4}$
8. Save time by defining $y=\frac{x}{4}+3$ and solve the resulting quadratic. Time taken 1:28.
$2y^2-y-36=0$
$(2y-9)(y+4)=0$
$x=4(y-3)=-28$ or $6$
9. Apply conservation of momentum to work out the new speed and then the kinetic energies. Time taken 0:38.
Momentum before $=8\times4-2\times1=30kgms^{-1}$ therefore the speed after is $3ms^{-1}$
Applying $\frac{1}{2}mv^2$ the Kinetic Energy before is $65J$ and after is $45J$.
10. Note that the constant term cancels. Expand in one step then complete the square. Time taken 0:51.
$3x^2+18x$
$3(x+3)^2-27$
11. Use the graph to determine the final speed then apply Force as the rate of change of momentum. Time taken 3:23.
The gradient of the line is $\frac{30}{5}=6$ so the rate of change of momentum is $\frac{6}{5}\times 800=960N$
12. Start with $N=\frac{k}{t^3}$. Leave $k$ as a product to aid cancellation. Time taken 0:52.
$N=\frac{k}{T^3}$
$k=250\times8^3$
A $700\%$ increase is the same as mulitplying by $8$.
$8\times250=\frac{250\times8^3}{x^3}$
$x^3=64$
13. Try to find the wavelength from the information given without too much delay. The wave travels $vt$ but the distance between $P$ and $Q$ needs to be taken into account. Then apply $v=f\lambda$. Time taken 1:58.
The wavelength consists of the distance between $P$ and $Q$ which is $6$ plus the distance travelled by the wave in the time interval given in the question.
$\lambda=6+vt=2v$ where $v$ is the speed of the wave and the final step has come from $v=f\lambda$.
$6=\frac{6v}{5}$
14. Define the correct original price to be (say) $X$. Use percentage multipliers to work out the incorrect original price in terms of the correct original price, subtract $X$ and equate the result to $15$. Time taken 5:55 (several numerical/conceptual slips).
Let the sale price be $S$ and the incorrect price be $X'$
$S=0.75X$
$X'=1.25\times0.75\times X$
$X-X'=(1-1.25\times0.75)X$
$15=(1-\frac{5}{4}\times\frac{3}{4})X$
$X=15\times16$
15. Use energy at the start - energy at the end = energy wasted. Time taken 1:29.
The work done is Kinetic Energy at the start plus the Potential Energy lost as a result of the fall minus the Kinetic Energy at the end.
$40\times40^2+2000\times80-40\times5^2$
$64000+1600000-1000$
16. Visualise $SQ$ by inspection and apply trigonometry to the rightmost triangle. Time taken 0:47.
$SQ=\sqrt{y^2-x^2}$. Retain this information or write it on the diagram.
$sin61=\frac{SQ}{z}$ and the answer follows.
17. The energy at the start is elastic potential which is converted to gravitational potential and kinetic energy. Time taken 1:38.
Halve $k$ in your head to give $10\times0.2^2=0.5\times0.2+\frac{0.05}{2}\times v^2$
$v=\sqrt{\frac{1.5\times0.2\times2}{0.05}}=\sqrt{\frac{15\times4}{5}}$
18. Draw a rough diagram and visualise the two possible squares (whose orientations will be at $45^{\circ}$ to one another). Time taken 1:15.
The distance between the points is $\sqrt20=2\sqrt5$. When this is the side of the square we have a perimeter of $8\sqrt5$. When this is the diagonal of the square, the square is smaller by a scale factor of $\sqrt2$.
$8\sqrt5-4\sqrt2\sqrt5$
19. Starting from Newton's second law, rewrite the mass as some initial mass minus a constant times time and rearrange for the acceleration. Time taken 1:16.
$a=\frac{F}{m}=\frac{F}{m_0-\alpha t}$. Now make a sketch of this; $a$ starts at $\frac{F}{m_0}$ and rises to an asymptote as $t\rightarrow\frac{m_0}{\alpha}$ which is convex which reveals the answer to be $A$.
20. Write the right-hand term of the quadratic formula and equate to $3$. Time taken 1:09.
Visualise the quadratic formula $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$. The solutions are the same distance either side of a middle (median value). The middle value is $-\frac{b}{2a}$ and the distance either side is $\frac{\sqrt{b^2-4ac}}{2a}$. Therefore this last expression is equal to $3$.
$\frac{\sqrt{p^2+32}}{4}=3$
$p^2=144-32$
$p^2=112$
Part B

21. The energy at the start is kinetic and gravitational potential, changing to kinetic energy and work done against friction. Time taken 0:49.
$\frac{1}{2}mv_1^2+mgh=\frac{1}{2}mv_2^2+WD$
22. Substitute $1$ and $2$ in and solve the resulting equations. Time taken 0:40.
$a+b=7$
$16+8a+4b-20=0$ or $2a+b=1$
$a=-6$ and $b=13$
23. The pressure is the same at both pistons and is equal to force/area. Note that the area has gone up by a factor of 9. Apply work done = force $\times$ distance to work out how the distance moved by piston $Y$ should relate to that travelled by piston $X$. Time taken 0:59.
$P=\frac{F}{A}$ and since the area of the second piston is $9$ times that of the first, the force must be $36\times9$ which reveals the answer to be $G$ or $H$. Looking at the answers, the two possibilities are that the second piston moves less for or further than the first. Mentally applying conservation of energy in the form of $Force\times Distance$ shows that there is no way the distance could be increased as well as the force, so the distance moved by the second piston must be smaller.
24. I sketched this but there was no need in retrospect as one of the functions is clearly beneath the other for the whole integral. Time taken 1:26 (inefficient method and numerical slips).
$\int_1^3\frac{x^2}{2}dx=[\frac{x^3}{6}]^3_1=\frac{26}{6}=\frac{13}{3}$ is the area above the axis and below we have a trapezium of area $\frac{1}{2}(1+3)\times2$ giving the answer $\frac{25}{3}$. With hindsight it likely would have been quicker to bring the lower function into the integral, so $\int_1^3\frac{x^2}{2}+xdx$ etc.
25. Determine the frequency from the graph, apply $c=f\lambda$ and note that the speed in water is greater than that in air which means the wave will be more 'stretched out' . Time taken 1:22.
$f=\frac{1}{4\times10^{-3}}=250Hz$
$\lambda_{air}=\frac{30}{25}=\frac{6}{5}$
Since the wave travels faster in water, its wavelength will be a factor of $5$ greater than this.
26. Imagine what will happen to a line with gradient greater than $1$ - its gradient after the reflection will be between $0$ and $1$. Time taken 0:08.
Thinking of the gradient as change in $y$ divided by change in $x$, if we reflect in the line $y=x$ these are swapped and any gradient becomes its reciprocal.
27. Try not to be overfaced by the text and apply $F=BIl$ and moment $=$ force $\times$ perpendicular distance from pivot. Time taken 1:37.
$0.05\times0.6\times50\times0.04\times0.15$. At this point I looked at the answers and saw how they were often different in terms of the leading digits and wrote:
$5\times6\times2\times1.5$ which is the wrong order of magnitude but enough work to realise rapidly that the answer starts with a $9$ and therefore no need to perform any further calculations.
28. Make two equations involving the sum of the arithmetic series, one for $20$ terms and the other for the first $40$ terms and solve. Time taken 1:24.
$10(2a+19d)=50$
$20(2a+39d)=0$ since the first $40$ terms sum to $0$.
$2a=-39d$
subtracting the first two equations we have $-20d=5$ and from this $d=-\frac{1}{4}$ and $a=\frac{39}{8}$. Summing $100$ terms gives:
$50(\frac{39}{4}-\frac{99}{4})=25\times30$
29. Conserve energy - the work done goes into increased kinetic energy and work done against the gravity (in this case it's best to think of work done against the component of weight acting down the slope). Time taken 1:38.
$30\times5=1.5(7^2-3^2)+5W$
evaluating the bracket as $40$ in my head and dividing by $5$:
$30-W=1.5\times8$
$W=30-12$
30. Draw a sketch and, taking the base of the triangle to be vertical, write this base in terms of $m$ and calculate the height as $2$ and solve. Time taken 2:22.
Substituting $(2,4)$ into the equation of the line and the equation for its reciprocal yields the following two intercepts respectively:
$4-2m$
$4+\frac{2}{m}$
The distance between these is $2m+\frac{2}{m}$ so we have, applying $\frac{1}{2}bh$:
$\frac{1}{2}(2m+\frac{2}{m})2=5$
$2m^2-5m+2=0$
$(2m-1)(m-2)=0$
31. Use $P=IV$ to work out the current then $P=I^2R$ for the power. Time taken 1:27.
$I=\frac{120000}{24000}=5$
Using $R=\frac{\rho L}{A}$:
$I^2R=25\times2\times\frac{2.5\times10^{-7}\times8000}{1\times10^{-4}}$
$2.5\times8\times50$
32. Note that the information given about the sequences implies that their common ratios are negatives of one another. Work out these common ratios and the first term then apply $S_{\infty}=\frac{a}{1-r}$. Time taken 3:27.
$a_1r_1^2=a_2r_2^2=4$
$a_1r_1^4=a_2r_2^4=2$
$r_1=\frac{1}{\sqrt2}$ and $r_2=-\frac{1}{\sqrt2}$
$a_1=a_2=8$
$\frac{8}{1+\sqrt2}-\frac{8}{1-\sqrt2}=8\sqrt2(\frac{1}{\sqrt2+1}-\frac{1}{\sqrt2-1})=16\sqrt2$
33. Work out the time taken to stop the ball, then use the average velocity to work out how far the ball travelled while it was being slowed down then double the result. I recommend keeping $a$ until the last step and focus on the leading digits of the answer rather than its precise value. Time taken 2:48.
$t=\frac{24}{a}$
The total distance is double the average speed multiplied by the time taken to stop:
Distance$=2\times12\times\frac{24}{a}=\frac{24^2}{6000}$ which starts $96....$ which enables you to select the correct answer.
34. After differentiation, the resulting quadratic requires a discriminant which is greater than zero. Time taken 1:23.
$3x^2+6\sqrt5px+3p=0$
$36\times5p^2>4\times9p$
$5p^2-p>0$
35. Form two equations using Hooke's law applied to each spring. Subtract these to take advantage of the $4cm$ given and calculate the spring constant then apply $\frac{1}{2}kx^2$. Time taken 1:47.
$2=kx_1$
$10=kx_2$
$x_2-x_1=0.04$
$8=0.04k$ so $k=200$
$x=\frac{20}{400}=0.05$
$EPE=\frac{1}{2}\times400\times0.05^2=0.5J$
36. Make a mental note that $cosx=0$ solves this equation. Use $cos^2x+sin^2x=1$ to write the equation in terms of just one of $sinx$ and $cosx$ then draw a sketch. Time taken not recorded (probably less than a minute).
$cosx=0$ or
$14c^2+10s^2=13$ where $c$ and $s$ have been used instead of $cosx$ and $sinx$ to save writing time.
$4c^2+10=13$
$c^2=\frac{3}{4}$
$cosx=\pm\frac{\sqrt3}{2}$. Now we have three values of $cosx$, each yielding $4$ solutions in this interval.
37. Equate the change in momentum to the area under the graph to find the velocity and apply $KE=\frac{1}{2}mv^2$. Time taken not recorded (probably about 1.5 minutes).
$m\Delta v=\frac{1}{2}\times0.2\times20=2$
$\Delta v=\frac{4}{5}$
$\frac{1}{2}\times2.5\times(\frac{4}{5})^2=\frac{4}{5}$
38. If it helps to cut down the amount you write, define $log_{10}x$ as $y$ and don't fall into the trap of thinking that the logarithm of a number can't be negative. Time taken 1:30.
$4y^2+y-3=0$
$(4y-3)(y+1)=0$
$y=\frac{3}{4}$ or $-1$
$\frac{3}{4}-1=-\frac{1}{4}$
39. Apply Kirchhoff's laws (mentally, not written down) to realise that the voltage around the lower middle loop must be $0$ then use potential dividers. Time taken not recorded (probably about 2 minutes).
Defining $V_{200}$ to be the potential difference across the $200\Omega $ resistor:
$\frac{16\times R}{R+1200}=\frac{6\times200}{100+200}$ which gives $R=400\Omega$
40. Read the question carefully and differentiate twice. Note that the third derivative is negative so the only stationary point must be a maximum. Time taken 1:10.
$\frac{dy}{dx}=-4+6\sqrt x-2x$
$\frac{d^2y}{dx^2}=\frac{3}{\sqrt x}-2=0$
$x=\frac{9}{4}$
$\frac{dy}{dx}=-4+\frac{6\times3}{2}-\frac{9}{2}$


Section 2

1. Work out the spring constant of the combination and then the load. Note that both springs each support this load because they are in series. Time taken 2:07.
$k_{total}=\frac{1}{\frac{1}{1}+\frac{1}{3}}=\frac{3}{4}$
$load=mg=\frac{3}{4}\times6=1\times x$
2. Apply $R=\frac{\rho L}{A}$ and divide by $12$. Time taken 0:46.
$R_{single}=\frac{4.8\times10^{-7}\times15}{\pi\times4\times10^{-8}}=\frac{12\times15}{\pi}$
3. Note that the time taken is enlarged by a factor of the refractive index. Apply this and use $Time=\frac{Distance}{Speed}$. Time taken 1:05.
$t=\frac{L}{c}\times n$
$n=\frac{1}{sin60}=\frac{2}{\sqrt3}$
4. Work out the mass of the cube, followed by the extension of the spring in terms of $k$ then apply $EPE=\frac{1}{2}kx^2$. Time taken 3:57.
$m=0.2^3\times2000=16kg$
$x=\frac{160}{k}$
$3.2=\frac{1}{2}k\frac{160^2}{k^2}$
$k=\frac{160^2}{2\times3.2}=\frac{1600}{32}\times\frac{160}{2}=4000Nm^{-1}$

5. Evaluate how long the flight must be from the information given then apply SUVAT horizontally and vertically. Time taken 6:17.
Resolving the initial velocity we have a vertical component of $10ms^{-1}$ and a horizontal component of $10\sqrt3 ms^{-1}$.
Vertically, the projectile loses $10ms^{-1}$ every second, therefore the time of flight is $1.4s$
$d=10\sqrt3t=14 ms^{-1}$
$h=10t-5t^2=14-5\times1.4^2=14-\frac{49}{5}$ which is just above $4$, enabling you to select the correct answer without working out the exact value.
6. Apply the same definition of amplitude for a transverse wave (the maximum displacement from the equilibrium position) to this longitudinal wave. Time taken 2:40.
This maximum displacement occurs for the third particle from the left (and the third particle from the right) which is $0.7m$
7. Using the energy given, work out the initial velocity of the spaceship. Then calculate the new velocity after the impulse, find the change in Kinetic Energy and divide by the time taken. Time can be saved by using difference of two squares. Time taken 2:08.
$10^{12}=4\times10^4\times v^2$
$v^2=2.5\times10^7=0.25\times10^8$ so $v=0.5\times10^4=5000 ms^{-1}$
From the information in the question, the new velocity is $4000 ms^{-1}$
Rate of loss=$\frac{\frac{1}{2}mv_i^2-\frac{1}{2}mv_f^2}{2}=20000(5000^2-4000^2)=20000(9000)(1000)$ and only one of the answers starts $18...$.
8. Apply $Pressure=\frac{Force}{Area}$. Time taken 0:44.
Pressure$=\frac{\frac{\sqrt3x^2}{4}\times3x\times\rho\times g}{3x^2}$ which cancels straightforwardly to give the answer.
9. Form two equations from the information given and solve. Time taken 1:21.
$25m_a=15m_r$
$30m_o=10m_r$
$\frac{m_a}{m_o}=\frac{15}{10}\times\frac{30}{25}=\frac{3\times3}{5}$
10. Apply $Power=Force \times Velocity$ to work out the resistive force then add this to the component of weight down the slope. Time taken 1:14.
$P=Fv$
$\frac{900}{12}=F$
$sin30=\frac{1}{2}$ so the component of weight down the slope is $\frac{850}{2}$
$\frac{900}{12}+\frac{850}{2}=75+425$
11. Work out the possible resistances in terms of a unknown resistance, say $R$, and use trial and improvement to ascertain which of the possibilities correspond to those given in the question. Time taken 6:22 (Question misread in that I tried to do this with four resistors instead of 3).
The possibilities are all three in parallel with each other, two in series in parallel with the third, two in parallel in series with the third and all three in series with each other with the following resistances respectively:
$\frac{R}{3}$
$\frac{2R}{3}$
$\frac{3R}{2}$
$3R$
A bit of trial and improvement reveals the second of these to be $8\Omega$ and the third to be $18\Omega$ giving $R=12\Omega$
12. Use Ohm's law to work out the resistance of the LDR at the initial intensity of light. Note that the resistance of the LDR must increase as a result of the dimming of the light and work out the potential differences across the two components then apply potential divider theory. Time taken 2:06.
$I=\frac{V}{R}=\frac{100}{4000+R}=5\times10^{-3}$
$100=20+5\times10^{-3}R$ giving $R=16000$
By potential dividers, the potential difference across the fixed resistor is $20V$. When this halves, $90V$ must be across the variable resistor and applying potential dividers again shows that the resistance of it must be $9$ times that of the fixed resistor, so $36000\Omega$. Note that the question asks for the change in this resistance, not its new value.
13. Noting that the cord now takes the shape of an isosceles triangle, it can be observed by inspection that its length had increased by a factor of $\sqrt2$. The extension and then the Elastic Potential Energy follow from this. Time taken 3:02.
The original length is $2r$ extended length is $\sqrt2\times2r$.
Energy stored $=\frac{1}{2}k(2\sqrt2-2)^2r^2=k(6-4\sqrt2)r^2$
14. Recall that force is the rate of change of momentum. Time taken 0:48.
If $F=\frac{dp}{dt}$ then we can integrate this to give the momentum.
$p=[Xt+\frac{2}{3}Yt^{\frac{3}{2}}]^T_0$ and the factor of $\frac{2}{3}$ can help you to spot the answer without any further working.
15. Differentiate to find the velocity as a function of time, from which you can work out the initial and final velocity. Applying difference of two squares may save some time in the final calculation. Time taken 1:05.
$v=4+2t$
$v$ goes from $4$ to $24$.
$\frac{1}{2}m(v_f^2-v_i^2)=\frac{3}{2}(24^2-4^2)=\frac{3}{2}\times28\times20$
16. The relation between the refractive indices in media $P$ and $R$ are the same whether the light travels through $Q$ or not. Use the ratios given to find the ratio of speeds in medium $P$ to $R$ and note that the ratio of refractive indices will be this ratio reversed since speed is inversely proportional to refractive index. Once this has been obtained, Snell's law can be applied directly to media $P$ and $Q$. Time taken 2:40.
$n_Psin\theta=n_Qsin\alpha=n_Rsin45$
$sin\theta=\frac{n_R}{n_P\sqrt2}$
Multiplying the first ratio by $3$ and the second ratio by $\sqrt5$ gives the ratio of speeds of light between media $P$ and $R$ to be $6:6\sqrt5$ or $\sqrt6:\sqrt5$. Therefore the light travels faster in medium $P$ and $\frac{n_R}{n_P}=\frac{\sqrt6}{\sqrt5}$ so $sin\theta=\frac{\sqrt3}{\sqrt5}$.
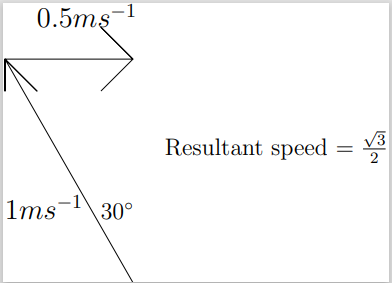
17. The horizontal paths are straightforward to deal with but for the vertical paths, form right-angled triangles to work out the resultant speed. Time taken 1:24.
$ST:\frac{30}{1.5}$
$UR:\frac{30}{0.5}$
$RS$ and $TU:$ the speed is the third side of a right-angled triangle with hypotenuse $1$ (the swimming speed) and second side $0.5$ (for the river). See the picture below for an illustration of this. The time in each case is $\frac{60}{\sqrt3}$
Therefore the total time is:
$60+20+40\sqrt3$
18. Use the Young's Modulus formula to work out the extension then apply Energy stored $=\frac{1}{2}Fe$. Time taken 2:10.
$Y=\frac{Fl}{Ae}$
$\frac{2\times10^{11}}{8\times10^8}=\frac{4}{e}$
$e=\frac{16}{1000}$
$F=8\times10^8\times2\times10^{-4}=1.6\times10^5$
By inspection, it can be seen that $\frac{1}{2}Fe$ must start $128...$ and the answer can be selected from here.
19. Note that the net displacement is zero therefore the journey is 'there and back again' with a greater speed on the return journey. Time taken 0:58.
When the displacement is increasing, the velocity is small and positive. When it is decreasing the velocity is negative and has a larger absolute value. Try not to confuse this with a sketch of velocity against time and note that there cannot be any slanted lines in the sketch since the velocity changes abruptly only.
20. Find the potential difference across the variable resistor and multiply by $I$ to yield an expression for the power dissipated. Differentiate this and set it equal to zero to find a relationship between $E$, $k$ and $I$. Substitute this into an expression for $R$ found by applying Ohm's law to the potential difference across the variable resistor. Use the relationship between $E$, $k$ and $I$ again to find an answer in terms of $k$ and $E$. Time taken 10:13.
Apply Ohm's law to the variable resistor: $I=\frac{E-kI^3}{R} (equation$ $1)$
Using $P=IV$ the power dissipated in it is:
$P=IE-kI^4$
and differentiating yields:
$\frac{dP}{dR}=E\frac{dI}{dR}-4kI^3\frac{dI}{dR}=0$
there is no need to obtain an expression for $\frac{dI}{dR}$ except to note that it is not $0$.
$E=4kI^3 (equation$ $2)$
From $(equation$ $1)$, we have:
$R=\frac{E}{I}-kI^2=4kI^2-kI^2=3kI^2$
but using $(equation$ $2)$ again, $I^2=(\frac{E}{4k})^{\frac{2}{3}}$ and the answer follows.